19+ a single vector by itself is linearly dependent
The correspondence xB - x is called the coordinate mapping. How do you know if a vector is linearly independent.

Us10189894b2 Rationally Designed Synthetic Antibody Libraries And Uses Therefor Google Patents
A single vector by itself is linearly dependent.

. A single vector by itself is linearly dependent. Hence 1vl is linearly independent. A single vector by itself is linearly dependent.
Point Check the true statements below. A set of vectors is linearly independent if and only if the equation. A basis is spanning set that is as large as possible.
D If x is in a vector space V and if a basis B for V contains n vectors then the coordinate vector of x for. If H Span b1bp then b1bp is a basis for H. A basis is a spanning set that is as large as.
The formal definition of linear independence. A single vector by itself is linearly dependent. A single vector by itself is linearly dependent.
Has only the trivial solution. If H spanb1 bp then b1 bp is a basis for H. In some cases a plane in R3 can be isomorphic to R2.
C 1 v 1 c 2 v 2 c k v k 0. False it would have to be the zero vector to be linearly dependent by itself. A vector cannot be linearly dependent because linear dependence is a property of a set of vectors not vectors themselves.
Advanced Math questions and answers. C A spanning set that is as large as possible is a basis. A vector v neq 0 itself is always linearly.
A single vector by itself is linearly dependentIf is in a vector spaceand if a basis Bfor vectors then the coordinate vector of for the basis B is incontainsThe number of pivot columns of a. The span of a vector is not a vector rather the set of linear combinations of that vector and thereby trivially linearly dependent. A A single vector is linearly dependent.
A basis is a spanning set that is as large as possible. If v 0 then the only scalar c such that cv 0 is c 0. Given a set of vectors you can determine if they are linearly independent by writing the vectors as the columns of the matrix A and solving.
In some cases the linear. This is kinda nitpicking though so lets move on to my. A linearly independent set in a subspace H is a.
2 points Check the true statements below. C A single vector by itself is linearly dependent. CIf H span b1.
Advanced Math questions and answers. B In an nxn invertible matrix the columns form a basis for R.
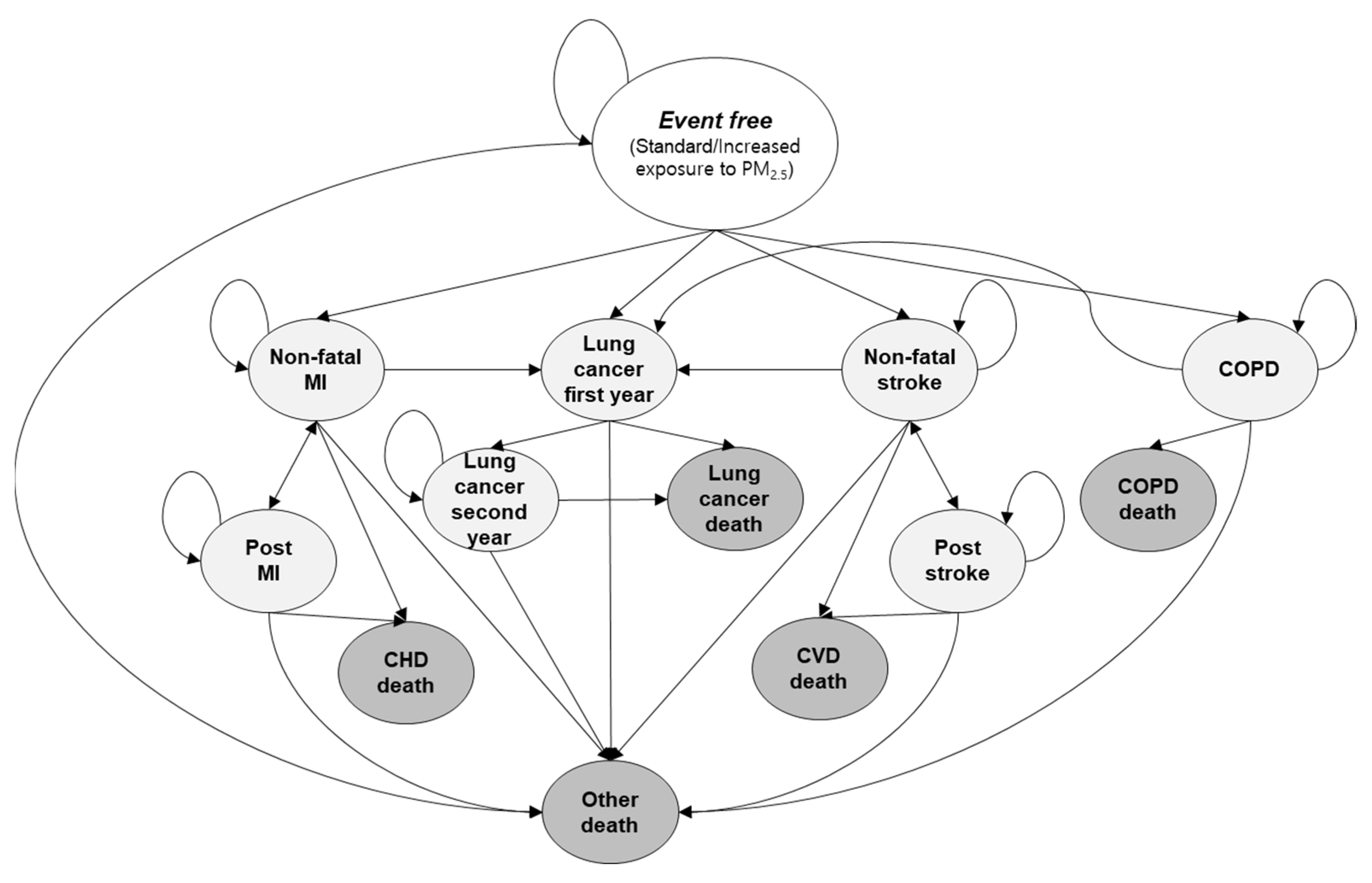
Ijerph Free Full Text Projecting Lifetime Health Outcomes And Costs Associated With The Ambient Fine Particulate Matter Exposure Among Adult Women In Korea Html

Adult Education Budget Funding And Performance Management Rules 2022 To 2023 Gov Uk
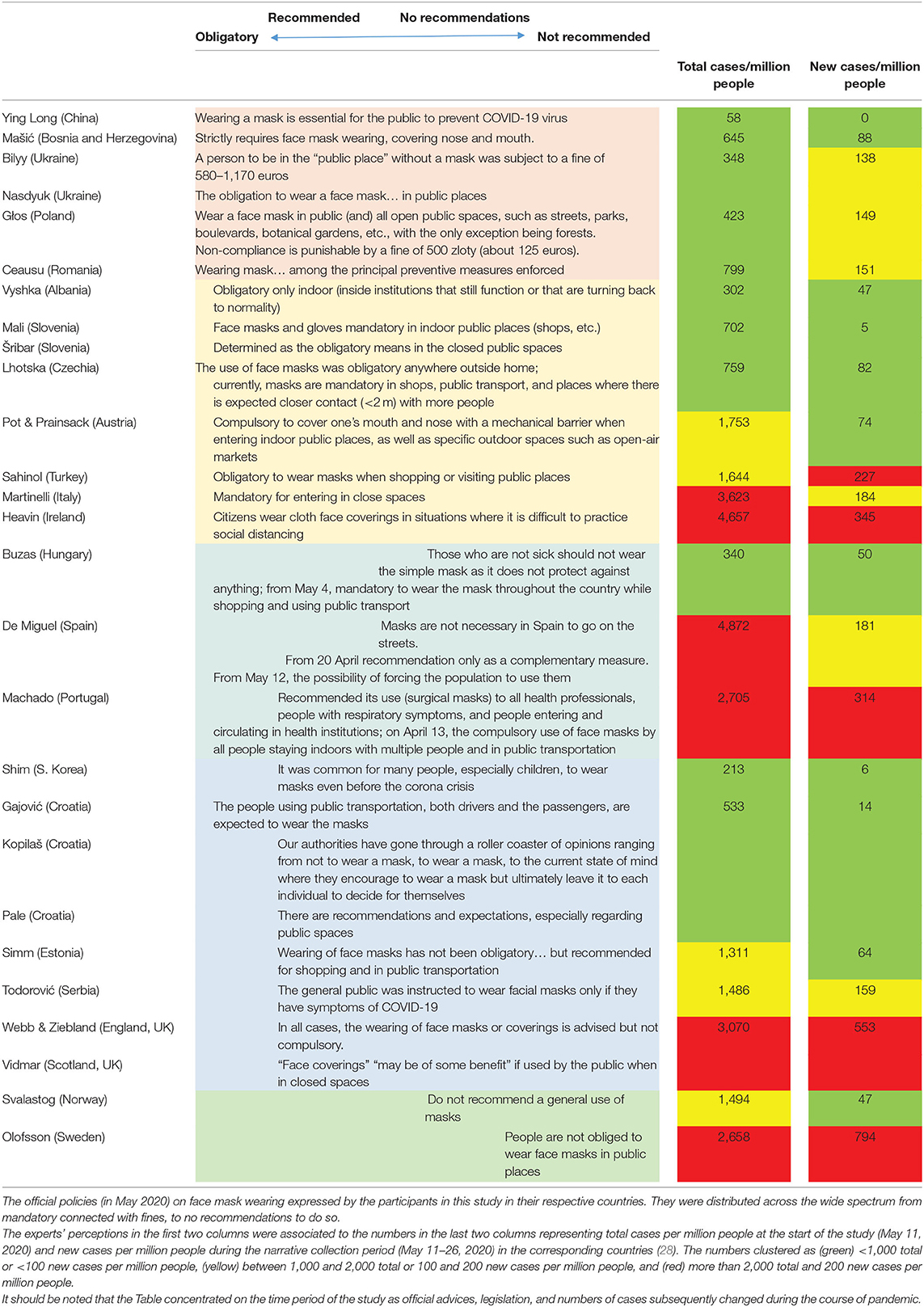
Frontiers Face Masks During The Covid 19 Pandemic A Simple Protection Tool With Many Meanings

In Vivo Characterization Of Emerging Sars Cov 2 Variant Infectivity And Human Antibody Escape Potential Sciencedirect

Surface Induced Dissociation Mass Spectrometry As A Structural Biology Tool Chemical Reviews
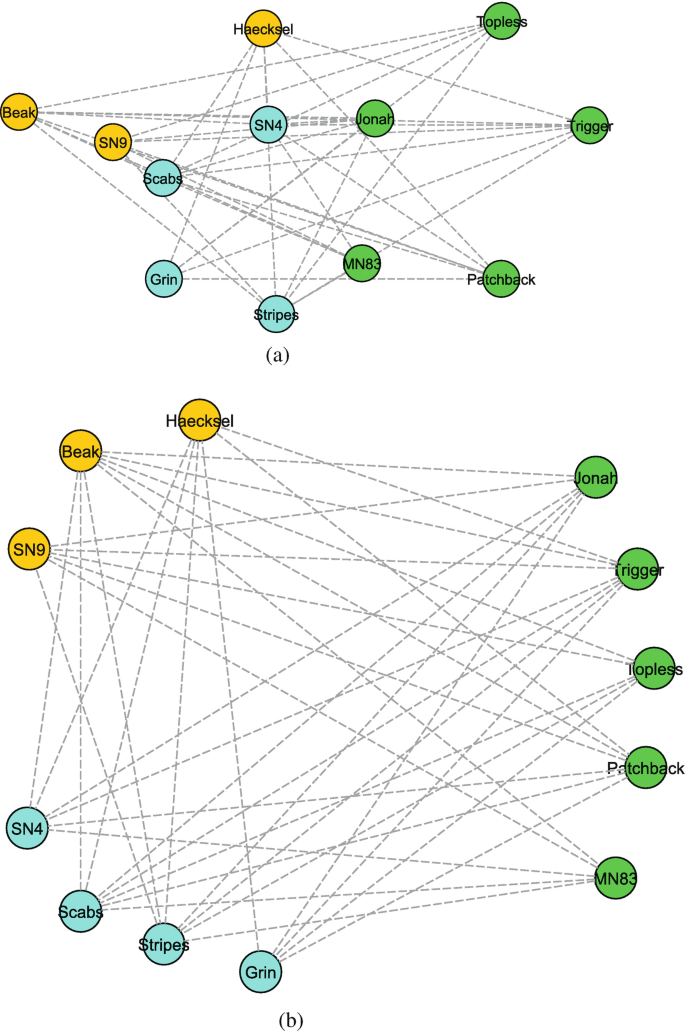
Business Network Analytics From Graphs To Supernetworks Springerlink

Organizational Speed In The Post Covid 19 Era Mckinsey
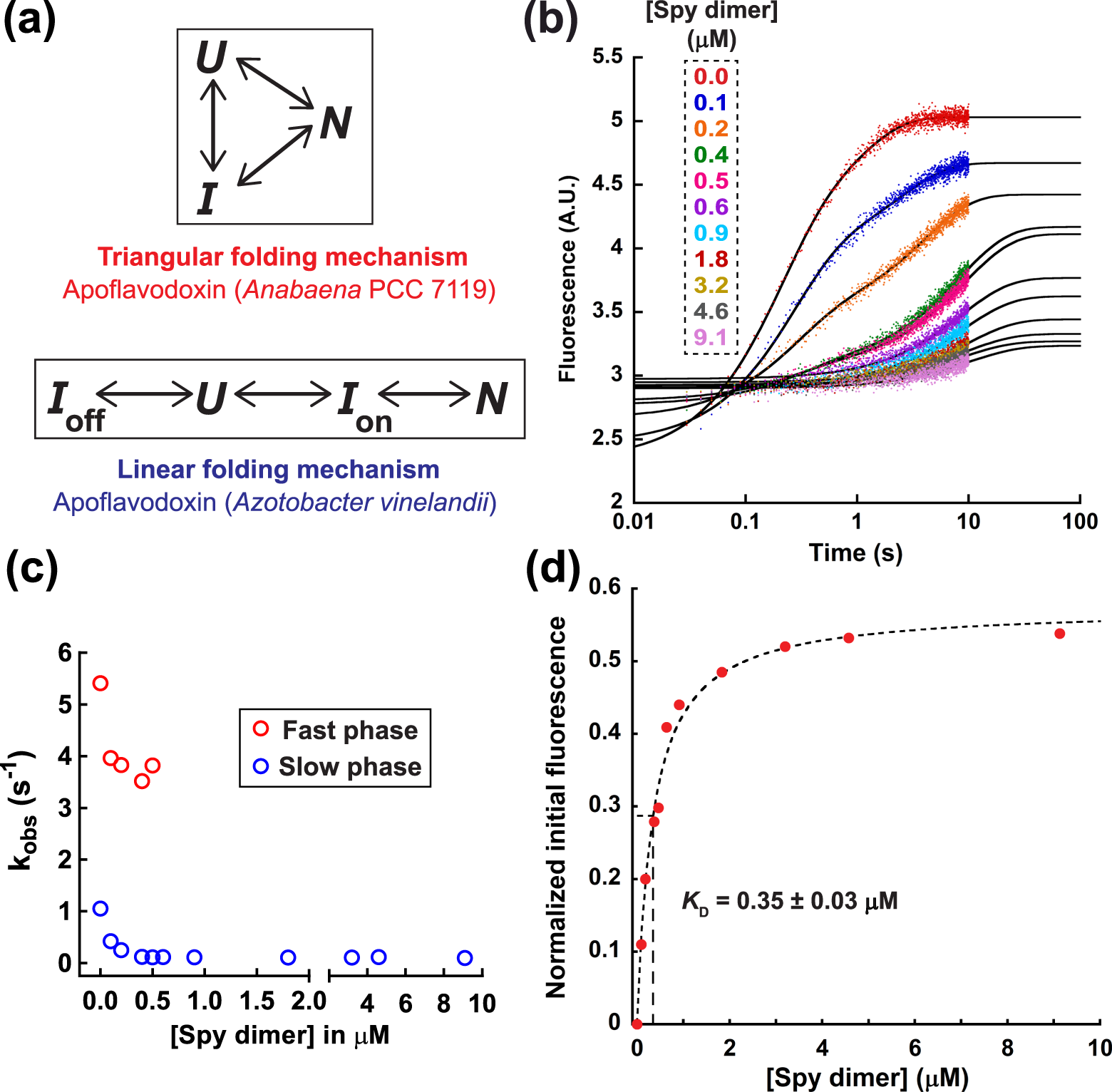
Mechanism Of The Small Atp Independent Chaperone Spy Is Substrate Specific Nature Communications
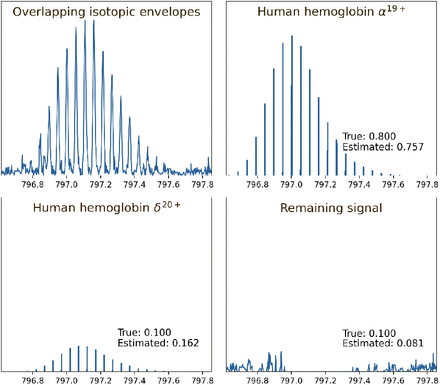
Masserstein Robust Linear Deconvolution By Optimal Transport Biorxiv

Linearly Independent Vectors Definition Deepai

Linear Independence Wikipedia

B Cell Overview Thermo Fisher Scientific Fr

Img Library Img Connect

Biochemical Characterisation Of Class Iii Biotin Protein Ligases From Botrytis Cinerea And Zymoseptoria Tritici Sciencedirect
Full Article An Empirical Analysis Of Efficiency In The Indian Gold Futures Market

Microheterogeneity Of Topoisomerase Ia Ib And Their Dna Bound States Acs Omega

Tetratopic Terpyridine Building Unit As A Precursor To Wheel Like Metallo Supramolecules Inorganic Chemistry